
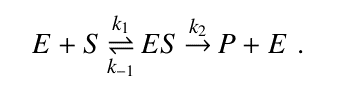
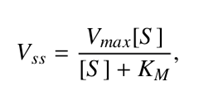
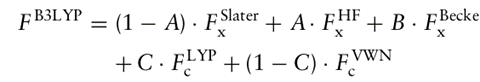
Enzymes play a central role in life, catalysing many chemical and biological processes occurring in nature. Understanding how enzymes catalyse their reactions is a problem of major importance, both from a fundamental and a practical perspective, with application in a variety of areas, from more basic research that aims to understand how different events occur in the cell, to the development of new treatments for important diseases, and in industrial biocatalytic application especially in enzyme engineering.
In 1913, Leonor Michaelis and Maud Menten introduced the initial rate method for kinetic analysis. According to Michaelis-Menten (MM) mechanism, enzyme E binds with substrate S to form an enzyme-substrate complex ES, which either dissociates irreversibly to form product P, regenerating the free enzyme E or dissociates reversibly to release the substrate
Assuming a steady state approximation I.e., d[ES]/dt=0, the mean rate of product formation yields
the celebrated MM equation is a valuable tool providing a quantitative framework for the optimization of enzyme performance.
Usually, laboratory enzyme assays are used to measure the rate of enzyme reactions. Because enzymes are not consumed by the reactions they catalyse, enzyme assays usually follow changes in the concentration of either substrate or products to measure the rate of reaction. Spectrophotometric assays observe change in the absorbance of light between products and reactants; radiometric assays involve the incorporation or release of radioactivity to measure the amount of product made over time. Other examples include different spectroscopic techniques, kinetic studies, studies with mutant enzymes, experiments in different pH conditions or temperatures, in the absence or presence of different metal atoms, among others. Such methods help to elucidate some of the structures and conformations adopted by enzymes along their reaction path and to identify some of the atoms and amino acid residues directly participating in their reactions. It also enables the determination of the kinetics of the reactions catalysed.
However, such methods often fail to present a full view of the enzymatic reaction, leaving many chemical questions unanswered.
Computational methods are being used to go beyond some of the limitations of the experimental methodologies, providing an alternative strategy to complement the information arising from this method. Many different computational methods have been used through the years to model enzymatic reactions.
QM approach:
The cluster approach for modelling enzymes is nearly three decades old. The basic idea of the cluster approach for modelling enzyme active sites and reaction mechanisms is to cut out a relatively small but well-chosen part of the enzyme and treat it with as accurate quantum chemical methods as possible. To account for the excluded rest of the enzyme, two simple approximations are used, namely the polarizable continuum model and a coordinate-locking scheme.
The most useful electronic structure method for treating large molecular systems during the past decades has been the hybrid DFT method with the B3LYP exchange correlation functional.
Today, the size of the active site models is typically in the order of 100–150 atoms. The protein surrounding that is not explicitly included, can affect the model in two main ways. First, the protein matrix can impose steric constraints on the various parts of the model. If not considered, this might lead to large artificial movements of the various groups, which can result in an incorrect description of the reactions, especially features like selectivity. Second, the surrounding can provide long-range polarization that can affect the computed energies. To account for these two effects, two basic approximations are used. To model the steric effects, a rather simple method is to lock certain key coordinates at the periphery of the model, typically where the truncation is made. This way, large artificial movements of the active site groups are prevented from taking place during the geometry optimizations and the overall structure is kept close to the experimental one. To model the electrostatic effects, polarizable continuum techniques are usually used. This assumes that the surrounding is a homogenous polarizable medium with some assumed dielectric constant. The solvation energies are usually obtained from single point calculations performed on the optimized geometries. The choice of this constant is somewhat arbitrary, but ε = 4 is usually considered to be a good representation of protein surrounding.
One of the challenges of using the cluster approach for modelling enzymes is the limited size of the active site models that can be treated with high accuracy quantum chemical methods. The models used today typically contain 100-150 atoms, which is small compared to the size of the entire enzyme. This limitation can result in an incomplete understanding of the reaction mechanism and selectivity of the enzyme, as the protein matrix and its long-range effects on the active site are not fully accounted for.
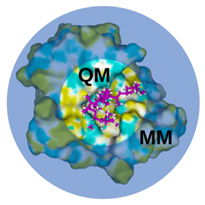
QM/MM method
QM/MM combines two computational methods: quantum mechanics, which is used to model the electronic structure and chemical reactions of a small portion of the enzyme (usually the active site), and molecular mechanics, which is used to model the larger enzyme molecule and the surrounding solvent. The QM/MM approach allows us to model the chemical reactions that take place in the active site of an enzyme, while considering the effects of the surrounding environment. This is important because enzymes are typically large, complex molecules that operate in an aqueous environment, and the behaviour of the enzyme is influenced by interactions with the surrounding solvent molecules.
The system is divided into a (small) QM region and an (usually much larger) MM region. The total energy of a QM/MM system can be expressed as
EQM and EMM are the energies of the QM and MM regions, respectively, calculated in a standard way at those levels. EQM/MM describes the interaction between the QM and MM regions and can be treated in various ways which are shown as below.
Type A: QM/MM implementations of type A use the simplest linking of QM and MM methods, involving a straightforward ‘mechanical’ embedding of the QM region in the MM environment. The interactions between the QM and MM regions are treated purely classically by MM, i.e. the QM system is represented by (MM) point charges in its interaction with the MM environment, meaning the polarisation of the QM region is not included.
Type B: Electrostatic interactions between the QM and MM regions are included in type B models using invariant atomic partial point charges in the MM region (from the MM force field) that enter the core QM Hamiltonian. Thus, the QM region is polarised by its MM environment.
Type C: Models of type C extend beyond type B by also including some polarisation of atoms in the MM region by the electric field generated by the QM region (compare to type D models below).
Type D: Models of type D are the most refined and sophisticated class of QM/MM method. They include the iterative, self-consistent mutual polarisation of the MM and QM regions
The most widely used QM/MM methods are of type B allowing the polarisation of the QM region by the MM region, including the charges of the MM groups in the QM calculation. The electronic structure calculation therefore includes the effects of the MM atoms.
EBoundary is a term to account for the fact that the system may have to be truncated for practical reasons (e.g. QM/MM calculations are computationally demanding, and it may not be possible or desirable to include the whole of an enzyme molecule).
The study of the enzymatic mechanisms provided by QM/MM methods enables an atomic-level analysis of the main interactions formed in the reactants, transition state (TS), and products. In addition, the structure of the TS and of the distribution of charge at this important intermediate and its variation in relation to the reactants and products offers an opportunity for the rational selection of proposals for site- directed mutagenesis. A popular objective is that of lowering the activation free energy of the enzyme, thereby improving the rate of the resulting reaction, making the enzyme potentially more appealing for industrial applications as a biocatalyst.
From the catalytic mechanism solved through the application of QM/MM methods, and by the analysis of the impact of the different amino acid residues around the active site in the wild-type enzyme, models are created, substituting key amino acid residues by others thought, for example, to stabilize better the transition state. The reaction is then simulated through QM/MM, and the resulting potential energy surface (PES) and activation free energies are compared with that of the wild- type enzyme. Several different possible mutations are normally evaluated by QM/MM, and the potential effects on the reaction-rate are estimated from the determination of the TS structures and associated energetics. Only the most promising alternatives are then tested experimentally.
We at Quantumzyme engineer high performing enzymes by extensively studying the enzymatic mechanism and effect of mutations by sophisticated methods like QM/MM and coming up the best performing enzymes.