Where there is QM/MM, there is Reaction Modelling!

1. Introduction

Traditionally, scientists used classical molecular mechanics (MM) and standalone quantum mechanics (QM) for reaction modelling. MM was great for quickly simulating molecular interactions, but it struggled with the complexities of chemical reactions like bond formation and breaking. QM, on the other hand, provided detailed insights at the electronic level but was too computationally expensive for large biological systems like enzymes. Semi-empirical methods and parameterized models were also in the mix, but they often fell short in accuracy and generalizability.

That's where QM/MM comes in, combining the best of both worlds. Imagine having the speed of MM and the precision of QM in one package! Arieh Warshel, Michael Levitt, and Martin Karplus made groundbreaking contributions by merging QM and MM methods, allowing them to tackle complex chemical systems using different levels of theory. This innovative approach led to the development of the hybrid QM/MM method, earning them the 2013 Nobel Prize in Chemistry for "the development of multiscale models for complex chemical systems.

So, how does this hybrid approach work? 

It uses QM for the reactive region (like active sites) to get high accuracy, while MM efficiently simulates the surrounding environment. This allows scientists to study complex biological reactions in realistic conditions, capturing both the dynamic behaviour of proteins and precise chemical changes. It's no wonder QM/MM has become an indispensable tool in enzymology and biocatalysis. QM/MM methods are incredibly powerful for studying systems where chemical reactions and physical processes depend on both the electronic structure of a small region and the influence of a larger environment. It's like having a microscope that can zoom in on the tiniest details while still seeing the big picture!

The QM/MM approach essentially divides a large biological macromolecule into three main subsystems:

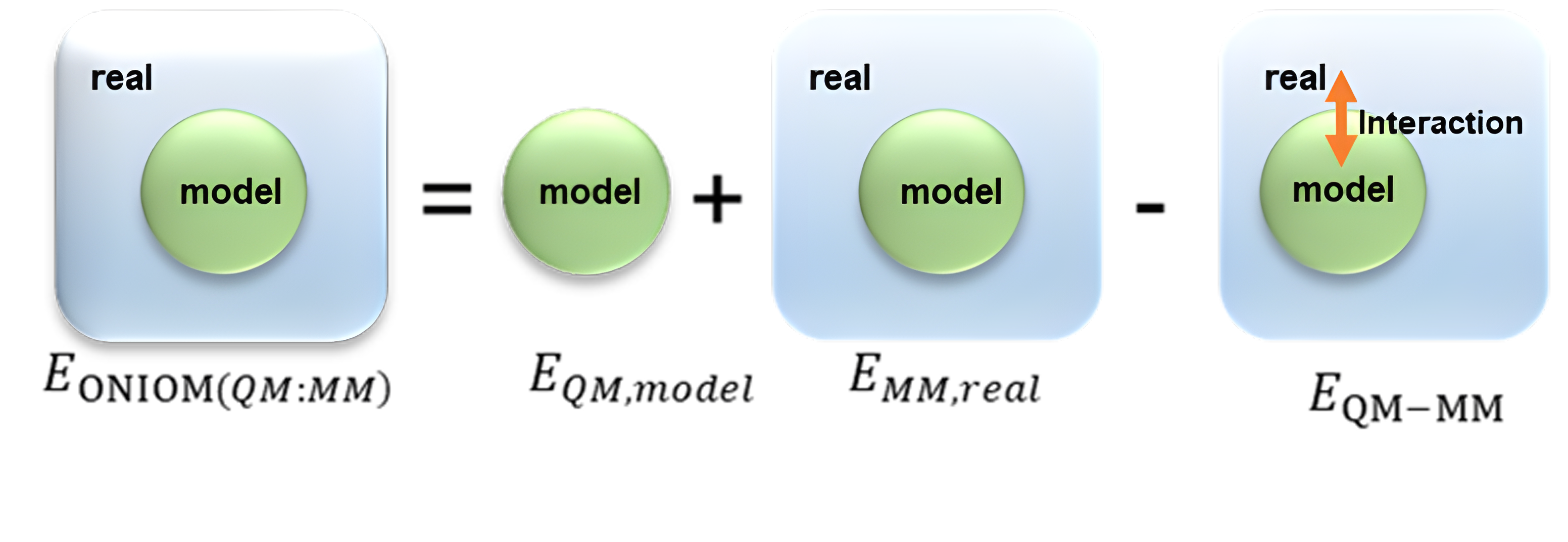
QM Subsystem: This is the chemically active region of the molecule, often including the active site where electronic changes occur. It is treated with a high-level quantum mechanical approach (EQM, model), which, although computationally intensive, provides the necessary precision.

MM Subsystem: The MM subsystem surrounds the QM region and includes everything else in the molecular environment nearby residues, solvent molecules, or even the entire protein structure in biological systems. Since this region often involves thousands of atoms, it’s treated using molecular mechanics, which is less computationally demanding but still does a good job of capturing interactions and maintaining structural stability.

Boundary Conditions:  In QM/MM boundary conditions play a vital role in ensuring the QM and MM regions interact smoothly. They prevent any weird artifacts or gaps at the QM/MM interface by ensuring forces and electronic interactions transition seamlessly. In QM/MM methods, boundary conditions essentially define how the QM and MM regions "talk" to each other, and there are four main types of these boundaries:

• Mechanical Embedding: The QM and MM regions are treated independently, and the interaction between them is represented through fixed MM point charges. This approach does not account for electronic polarization caused by the MM region. This approach is computationally efficient, making it suitable for studying large systems where electronic coupling between QM and MM regions is minimal. It is particularly useful for exploring systems with well-defined boundaries, such as enzyme active sites, where the MM environment provides structural stability without significantly altering the QM region's electronic properties.

   

• Electrostatic Embedding: This incorporates the MM charges into the QM Hamiltonian, allowing the QM region to respond to the electrostatic environment of the MM region, offering greater accuracy in capturing interactions. This method is particularly valuable when the QM region's behaviour is strongly influenced by its environment, such as in enzyme catalysis, where charged residues or polar solvents near the active site significantly impact reaction mechanisms.

   

• Polarization Embedding: This goes a step further by including mutual polarization, where both the QM and MM regions influence each other’s electronic structures dynamically. This is particularly important for systems with strong QM/MM interactions, such as enzyme active sites or solvent effects, as it provides a more realistic representation of their coupled behaviour. This embedding is crucial for systems where the electronic environment of the QM region and the polarization of the MM region are dynamically coupled, such as in highly charged or polar systems, complex enzymatic reactions, or processes involving strong solute-solvent interactions. By capturing these two-way effects, polarization embedding delivers a highly realistic representation of the system's behaviour.

   

• Covalent bonds across the QM/MM boundary: When it comes to hybrid QM/MM methods, things get really interesting, when the QM/MM boundary slices through a covalent bond. These directly connected atoms, known as junction atoms, can be a bit tricky to handle. Sometimes, you just cannot avoid the boundary crossing a bond. When it does, it is very important to cap the dangling bond of the QM atom; otherwise, it is like leaving the bond cut in half, which messes up the calculations. One clever way to handle this is using link atom schemes. These introduce an extra atom usually a hydrogen to stand in for the missing piece of the bond. This little helper atom bonds to the QM atom, saturates its valency, and ensures the system behaves realistically.

Figure 1. The illustration of the ONIOM QM/MM method typically depicts the system divided into three parts. Model (QM Part), Real (MM part) and boundary conditions

2. Applications of QM/MM Methods

QM/MM methods are powerful and widely used for exploring systems where electronic behaviour is the key. Some practical applications are listed below:

• Enzyme Biocatalysis: Researchers can focus on the chemically active regions, like the enzyme's active site and substrate, while considering the dynamic effects of the surrounding protein and solvent environment. QM/MM is especially valuable for studying reaction mechanisms, identifying transition states, and understanding the role of cofactors and key residues in catalysis. These insights are crucial for enzyme engineering, helping design more efficient or selective biocatalysts.

   

• Drug discovery and Design: QM/MM methods play a crucial role in drug discovery and design by aiding in the understanding of ligand-receptor interactions and optimizing drug candidates. These methods allow researchers to model the binding process at an atomic level, providing detailed insights into how potential drugs interact with their targets. By accurately simulating these interactions, QM/MM helps identify the most promising drug candidates and predict their efficacy and potential side effects.

   

• Photophysics and Photochemistry: QM/MM methods are invaluable in the fields of photophysics and photochemistry, where they are used to model excited states and light-driven processes in molecules. These methods allow scientists to understand how molecules absorb and emit light, which is crucial for a wide range of applications, from solar energy conversion to the development of fluorescent probes.

   

• Chemical Reactions in Solution: QM/MM methods are essential for studying chemical reactions in solution, as they capture reaction mechanisms influenced by solvent dynamics. In a solution, the behaviour of molecules can be significantly different from that in the gas phase due to interactions with solvent molecules. QM/MM allows researchers to model these interactions accurately, providing a detailed understanding of how solvents affect reaction pathways and rates.

3. Exploring Fluorescence Differences in WT UnaG vs. Mutants with QM/MM

We dive into a fascinating case study on the unique photoprotein UnaG and its mutant. We explore their optical properties to understand their photophysical behaviour better. By comparing the wild-type UnaG with its mutant, we uncover how specific amino acid changes affect UnaG's photophysical phenomena. This study showcases the power of QM/MM approaches in unraveling the complexities of photoproteins and their engineered variants.

Figure 2. The crystal structure of WT UnaG is shown in the left, with each domain of the protein labelled. The BLR molecule is located within the beta-barrel. The mutation site is highlighted with a red circle. On the right the structures of the UnaG Mutant. WT UnaG is green fluorescent while mutant is less/no

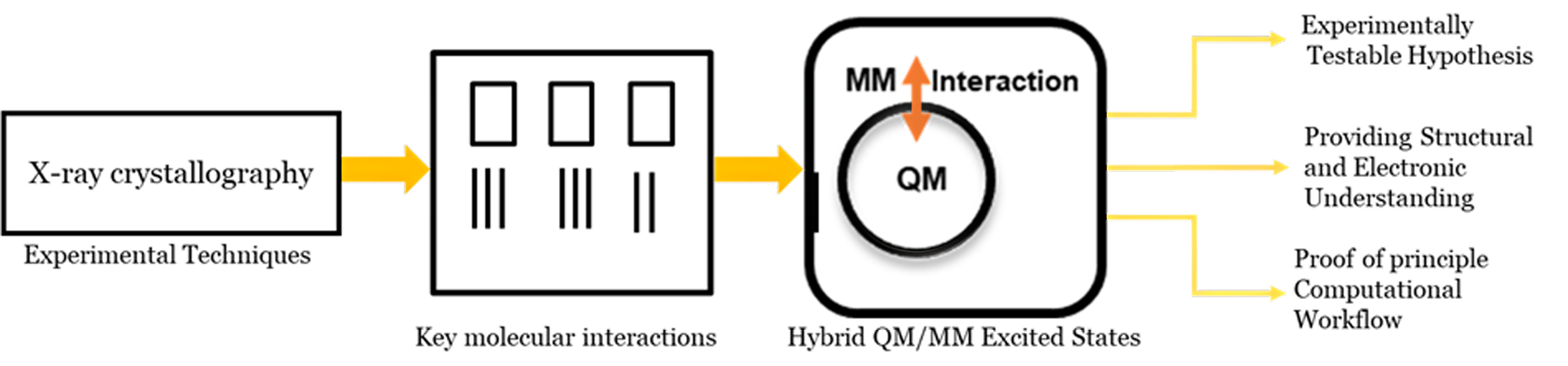
Unlike traditional fluorescent proteins such as GFP, UnaG emits green light (λemis=532 nm) only when it binds non-covalently to bilirubin (BLR), a natural metabolite of heme breakdown. This unique property makes UnaG an oxygen-independent and highly sensitive indicator of BLR, with potential applications in both medical diagnostics and scientific research. By introducing a single mutation in WT UnaG, the fluorescence of the protein is significantly reduced or even eliminated (Figure 2). The fluorescence of UnaG lasts up to 20 hours without reoxygenation which could be interesting to detect tumor cells5. In silico studies (QM/MM) have played a vital role in understanding UnaG fluorescence mechanics and exploring mutation that could diminish its properties. Experimental studies have shown that point mutations in the entry site cause structural changes that impact BLR orientation and binding, drastically reducing fluorescence. These changes reveal how specific residues control BLR conformational stability and how protein-ligand interactions influence fluorescence. Figure 3 shows a schematic of the methodology used for this case study.

Figure 3. Schematic representation of methodology. The structures obtained from experimental techniques were analysed to identify key molecular interactions. Subsequently, hybrid QM/MM excited-state calculations were performed and compared with the experimental studies.

ONIOM/TD-DFT calculations on UnaG WT and its mutant, with and without explicit water and amino acid residues within 4 Å of BLR, revealed interesting results. Theoretical λmax values of UnaG Mutant differ by only 8 nm without explicit water, while WT UnaG is slightly redshifted (λmax = 459) compared to mutant. With explicit water, the λmax values differ by 11 nm between the UnaG Mutant, with WT UnaG still slightly redshifted (λmax = 456). These findings highlight the significant impact of water molecules and surrounding amino acid residues on theoretical λmax values and the importance of accounting for them in computational studies. The emission peaks (λemis) for WT UnaG and its mutant are at 550 nm and 535 nm, respectively, with the mutant showing a lower emission intensity. The ONIOM TD-DFT method correlates well with experimental values, aiming to describe trends rather than absolute values (Table 1). The ONIOM TD-DFT method is presenting data which are in a correlation with the experimental values6. The aim of this study is to describe a trend and not absolute values (which obviously required an extended benchmark).

Table 1. Maximum absorption wavelengths (λmax), emission wavelength (λemis) of X-ray crystal structure of UnaG and its UnaGmutant systems using a two-layer ONIOM protocol (M06-2X/6-311+G(2d,p). Oscillator strengths (f) are indicated.

4. Challenges of QM/MM Methods for Biological Systems

Applying QM/MM methods to biological systems isn't without its challenges. One of the biggest hurdles is defining the QM/MM boundary, especially when it cuts through covalent bonds. It's like trying to slice a cake perfectly without messing up the layers – it requires careful handling to maintain electronic continuity.

Parameterizing the MM region and accounting for long-range interactions can also affect the accuracy of the results. Even though QM/MM is more efficient than full QM simulations, it still demands a lot of computational power, especially for large systems or dynamic processes. Imagine trying to solve a giant puzzle where every piece needs to fit perfectly – that's the kind of complexity we're dealing with.

Adding to the challenge, the inclusion of cofactors, metal ions, and enzyme flexibility makes the modelling even more intricate. Balancing accuracy with efficiency is a persistent struggle. Plus, limited experimental data can make validation tough, emphasizing the need for iterative model refinement and improved computational techniques.

Despite these challenges, the potential of QM/MM methods in advancing our understanding of biological systems is immense. It's a bit like exploring uncharted territory – difficult, but incredibly rewarding.

5. Conclusion and future perspectives

Computational enzymology is a rapidly growing field that gives us deep insights into the fundamental processes of biological catalysis at the atomic level. Imagine being able to see every tiny detail of how enzymes work, right down to the bonds they break and form. That's the power of QM/MM.

By accurately modelling these bond-breaking and bond-forming events within a realistic biological context, QM/MM is a game-changer for advancing green chemistry and industrial biocatalysis applications. It's like having a super microscope that lets us see and understand the intricate dance of molecules.

The future of enzyme catalysis research lies in the continued development and application of QM/MM methods. These methods provide a detailed understanding of both the atomistic and electronic aspects of enzyme function, driving innovations in enzyme engineering. Think of it as having a detailed map that guides us in designing better enzymes.

As computational power and techniques advance, QM/MM methods will become even more integral to unravelling the complexities of enzyme catalysis. They will help us harness the potential of enzymes for various scientific and practical applications, making them indispensable tools in our quest for knowledge and innovation